Regression/Training Demo:

This demo shows a few ways to build a PLS regression model and perform cross validation. If you want to see the gambit of regression methods included in ChemometricsTools check the regression shootout example.

There are a few built-in's to make training models a snap. Philosophically I decided, that making wrapper functions to perform Cross Validation is not fair to the end-user. There are many cases where we want specialized CV's but we don't want to write nested for-loops that run for hours then debug them... Similarly, most people don't want to spend their time hacking into rigid GridSearch objects, or scouring stack exchange / package documentation. Especially when it'd be easier to write an equivalent approach that is self documenting from scratch. Instead, I used Julia's iterators to make K-Fold validations convenient, below is an example Partial Least Squares Regression CV.

#Split our data into two parts one 70% one 30%
((TrainX,TrainY),(TestX, TestY)) = SplitByProportion(x, yprop, 0.7);
#Preprocess it
MSC_Obj = MultiplicativeScatterCorrection(TrainX);
TrainX = MSC_Obj(TrainX);
TestX = MSC_Obj(TestX);
#Begin CV!
LatentVariables = 22
Err = repeat([0.0], LatentVariables);
#Note this is the Julian way to nest two loops
for Lv in 1:LatentVariables, (Fold, HoldOut) in KFoldsValidation(20, TrainX, TrainY)
    PLSR = PartialLeastSquares(Fold[1], Fold[2]; Factors = Lv)
    Err[Lv] += SSE( PLSR(HoldOut[1]), HoldOut[2] )
end
scatter(Err, xlabel = "Latent Variables", ylabel = "Cumulative SSE", labels = ["Error"])
BestLV = argmin(Err)
PLSR = PartialLeastSquares(TrainX, TrainY; Factors = BestLV)
RMSE( PLSR(TestX), TestY )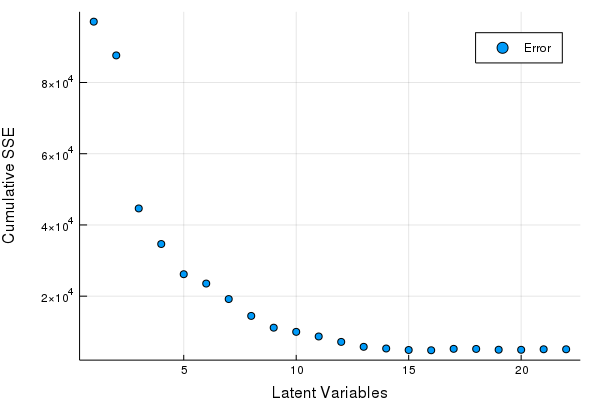

That's great right? but, hey that was kind of slow. Knowing what we know about ALS based models, we can do the same operation in linear time with respect to latent factors by computing the most latent variables first and only recomputing the regression coefficients. An example of this is below,

Err = repeat([0.0], 22);
Models = []
for Lv in 22:-1:1
    for ( i, ( Fold, HoldOut ) ) in enumerate(KFoldsValidation(20, TrainX, TrainY))
        if Lv == 22
            push!( Models, PartialLeastSquares(Fold[1], Fold[2]; Factors = Lv) )
        end
        Err[Lv] += SSE( Models[i]( HoldOut[1]; Factors = Lv), HoldOut[2] )
    end
end

This approach is ~5 times faster on a single core( < 2 seconds), pours through 7Gb less data, and makes 1/5th the allocations (on this dataset at least). If you wanted you could distribute the inner loop (using Distributed.jl) and see drastic speed ups!